GILBERT LIGHT EXPERIMENTS 51
commands him to rise. Two
concealed boys at T pull the rug and the boy appears to rise.
He can then be turned upside down and back again. You can
repeat with the boy lying down.
FUN BY DAY OR NIGHT WITH TWO MIRRORS
Experiment No. 41.
Magic money.
Stand the two mirrors
vertically on the table sidewise to a good light and place a
coin between them. Look over each mirror in turn into the
other (Fig. 74). Have you multiplied your money wonderfully?
Experiment No.42.
Magic lights.
Repeat the above in the dark with a lighted candle between the
mirrors
52 GILBERT BOY
ENGINEERING
(Fig. 75). Do you find many, many lights?
Experiment No. 43.
Magic army.
Put a number of lead soldiers
on a narrow strip of paper and draw them between the vertical
mirrors (Fig. 76). Do you see an immense army marching in
perfect order?
Experiment No. 44.
Magic dancers.
Cut out of paper or cardboard
a small figure of a man dancing. Attach him to a string and
make him dance between the mirrors in a good light (Fig. 77).
Do you find a multitude of dancers who keep time perfectly ?
Experiment No. 45.
Magic silver or copper mine.
Separate the mirrors by two
blocks, place them one above the other and face to face (Fig.
78); place a silver or copper coin on the lower mirror. Do you
find yourself looking down into a very deep hole with many
silver or copper coins in it?
Why you see Many Images in
Parallel Mirrors. You
GILBERT LIGHT
EXPERIMENTS 53
see many images between two
parallel mirrors because the image formed in one mirror is an
object in the other, and so on.
In Fig. 79, two mirrors, A and B, 4 inches apart are
facing each other and a candle between them is 1 inch from B and 3 inches from A.
In B the image Bl is formed 1 inch behind
B and in A the image Al is formed 3 inches
behind A.
Now image Al is 7
inches in front of B
and it forms an image B2
7 inches behind B;
similarly image Bl is
5 inches in front of A
and forms an image A2
6 inches behind A.
Again, A2 is 9 inches
in front of B and
forms an image B3 9
inches behind B, and
so on.
You see many images because the light which enters your eyes
has been reflected one or more times. If you are looking at Bl, the light which enters
your eye appears to come from Bl, but it comes from the candle and is
reflected from B.
54 GILBERT BOY
ENGINEERING
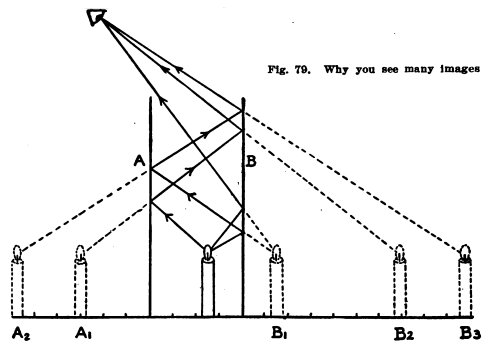
If you are looking at B2, the light appears to
come from B2, but B2 is an image of A1, and the light goes
from the candle and is reflected twice before it enters your
eye.
Image B3 is an image
of A2, which in turn
is an image of Bl, and
you
see B3 by means of
light which has been three times reflected. Similarly you
would see B4, B10, and B50 by means of light
reflected 4, 10, and 50 times.
It is good practice to locate the images in parallel mirrors
and to trace the paths of the light.
Why the Images become dim.
The images become dimmer the farther they are
GILBERT LIGHT
EXPERIMENTS 55
away: first, because some
light is absorbed by the mirrors at each reflection; and,
second, because the light has traveled a long distance in
being reflected back and forth between the mirrors.
Experiment No.46
The trench periscope.
To illustrate how the
periscope works, look over the top of a tall book as shown in
Fig. 80. Place one mirror against the book at an angle of 45°
and hold the second mirror above the book at the same angle.
Can you see over the top easily without being seen yourself?
Turn the upper mirror until it looks backward (Fig. 81), Can
you see back over your head, but is everything upside down ?
Turn the upper mirror until it looks sidewise (Fig. 88). Can
you see things, but are they turned on their sides?
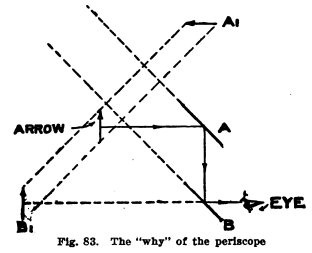
THE "WHY" OF THE PERISCOPE
Now let us see why the image is right side up in some cases and
not in others,
The mirrors in the regular
periscope are parallel to each other, and you can locate the
image in each mirror in turn as you
56 GILBERT BOY
ENGINEERING
did in the case of parallel mirrors.
Let the arrow, Fig. 83,
represent the object; its image in A is Al
and the top and bottom of Al
are as far behind the mirror extended as the top and bottom of
the arrow are in front.
Now let us suppose mirror B
to be extended as shown by the dotted line, then Bl is the image of Al in
this extended mirror and the top and bottom of Bl are as far behind B as the top and bottom of
Al are in front of B, and therefore Bl is right side up.
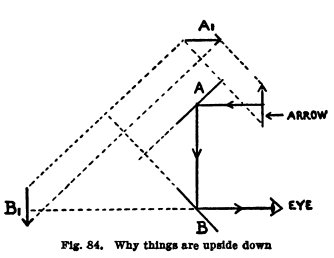
In the second case, the
mirrors are at right angles (Fig. 84). Al is the image of the
arrow in A extended
and Bl is the image
of Al in B extended; Al is on its side and Bl is inverted for the
reasons given above.
In the third case, the image is on its side in the upper
mirror, and since the lower mirror is parallel to this image,
the image in the lower mirror is still on its side.
Experiment No. 47.
To make a
GILBERT LIGHT
EXPERIMENTS 57
trench periscope.
Get a block of wood 4" X 4" X
6", measure down 1 inch from each end and draw a line across
diagonally. This line will be at 45° to the length of the
block. Cut the block through on this diagonal line, see right
side Fig. 85.
Now attach a mirror to each
diagonal face by means of tacks. Cut a piece of stiff
cardboard 17 inches wide and as long as you wish to make the
periscope. Tack this to the block, overlapping 1 inch on one
side. Paste the overlapping parts together. Cut a hole
3" opposite the upper mirror and a hole 2" X 2"
opposite the lower mirror, and your periscope is finished.
You can use this periscope in your trench battles; also you
can use it on a train to see forward without putting your head
out of the window. In this case, however, you should fasten
the window glass over one of the holes to keep cinders out of
your eyes.
FUN WITH MIRRORS AT DIFFERENT ANGLES

Experiment No. 48.
Mirrors at
different angles.
Stand the mirrors vertically and at right angles on the
table (Fig. 86) and place a lighted candle
58 GILBERT BOY
ENGINEERING
between them. Do you see four
candles, the real candle and three images?
Make the angle 60°. Do you see six candles, the original
candle and five images?
Make the angle 45°. Do you see eight candles?
Make the angle 30°. Do you see twelve candles?
There are 360° in a complete circle, and the number of candles
you see in each case is 360 divided by the angle between
the mirrors. For example, when the angle is 90°, you see
360
----
90
or 4 candles;
and when the angle is 60°, you see
360
----
60
or 6 candles; and so on.
Experiment No. 49.
A one-boy crowd.
Stand the mirrors at 90° and
put your face close to the mirrors. Are there four of you,
yourself and three images?
Repeat with the mirrors at the angles mentioned above. Do you
find yourself a crowd all in a circle?
Experiment No. 50.
Arrows.
Stand the mirrors at 90° on a
piece of white paper and draw an arrow pointing at one
of the mirrors. Do some of the arrows point in one direction
and some in the opposite direction? Keep one mirror in such a
position that the arrow points directly at it and move the
other mirror until the angle is 60°. Do the six arrows point
toward
each other in pairs?
Repeat with the mirror at the other angles mentioned above.
Experiment No. 51.
An infinite
number of candles.
Light a candle and stand the
mirrors close to it and gradually make them parallel. Do you
see very, very many candles?
When the mirrors are parallel the angle between them is 0° and
360
----
0
is infinity, so you should see an infinite
number of
GILBERT LIGHT
EXPERIMENTS 59
images. You cannot, because
some light is lost at each reflection and finally all is lost.
EDITOR'S NOTE: (Not
in the original text!) While the experts say it is possible to define
anything divided by zero as "infinity" as the author did
here, today most math whizzes choose to say that anything
divided by zero is "undefined." In this case, there
still are theoretically an infinite number of images, but
the math would probably not be considered "right"
today. It may be "splitting hairs" to even bring this
up, but the Notebook staff would not
want anyone unduly upsetting a math teacher!
Experiment No. 52.
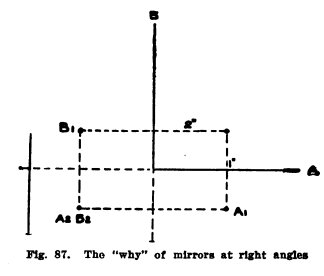
To locate the images in mirrors at an angle.
Draw two lines 4 inches long
at right angles to represent two mirrors at right angles (Fig.
87) and extend them backward by dotted lines to represent the
extended mirrors. Place a dot 1 inch from A and 2 inches from B, then image Al will be 1 inch behind A and image Bl 2 inches behind B. The
third image A2B2 is
an image of both Al
and Bl; it is 1 inch
behind A extended and
2 inches behind B
extended.
It is harder to locate the images when the angle is 60° or
smaller, but It will help you to know that the images are
always all on the circumference of a circle of which the angle
of the mirrors is the center.
Practice locating the images in mirrors at 60°.
Experiment No. 68.
The kaleidoscope.
The kaleidoscope (Fig. 88)
consists of two mirrors at an angle of 30° in a tube which has
an eye opening at one end and at the other a chamber
containing pieces of col-
60 GILBERT BOY
ENGINEERING
ored glass. When you look
through the tube and revolve it, the colored pieces of glass
make beautiful twelve-sided figures by multiple reflection.
Illustrate the working of the
kaleidoscope as follows: Draw two lines at an angle of
30° on a piece of white paper. Stand the mirrors on a block
above these lines with the angle toward a good light (Fig.
89). Now put pieces of colored paper and other small objects
on a strip of paper and draw the paper under the angle, while
you look down between the mirrors with your eye near the
angle. Do you see a series of twelve-sided figures?
ILLUSIONS
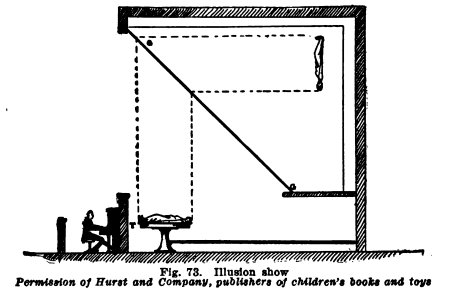
The Sphinx. This illusion shows an Egyptian
head without a body (Fig. 90). The hypnotist shows the
audience an empty box with a glass front. He closes and locks
the door over the front, places the box exactly on the center
of the table, unlocks it, opens the door, and, behold, there
is an
GILBERT LIGHT
EXPERIMENTS 61
Egyptian head in the box. The
hypnotist stands near the audience and addresses the head. "O
ancient Sphinx, awake! Awake! Awake !" The sphinx slowly opens
its eyes and stares straight ahead. The hypnotist then
addresses questions to it and it answers in very deep and very
dead tones, and so on. Finally the hypnotist locks the box,
brings it forward to the audience, opens it, and there is
nothing in it but a handful of ashes.
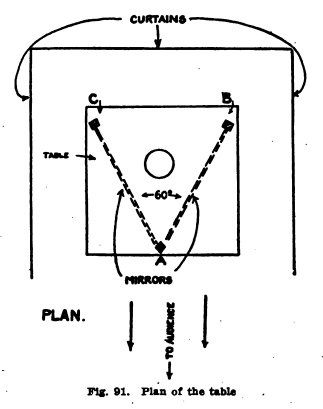
The mechanism of this illusion
is illustrated in Fig. 91. The table is on three legs. A, B, C, with mirrors at
60° between A, C, and
A, B. The curtains at
the back and sides are exactly alike, and to the audience the
images of the side curtains appear to be the back curtain, and
the space under the table appears quite empty.
Cabinet of Proteus.
The performer puts his assistant into the cabinet (Fig. 92),
closes the doors a moment, makes passes, open doors (Fig. 93),
and the assistant is gone. Closes doors again, makes passes,
opens doors, and out comes an entirely different man. Closes
doors again, makes passes, opens doors, and out comes a lady.
Closes doors again, makes passes, opens doors,
62 GILBERT BOY
ENGINEERING
and out comes assistant.
To the audience, the cabinet appears entirely empty
except for a post, C, with a strong light at the top. There
are, however, two hinged mirrors, ab and ab. Fig. 94, at an
angle of 60° and the post covers the angle. The sides and back
are exactly alike and the images of the sides in the mirrors
appear to the audience to be the back. The man, lady, and
assistant, of course, hide behind the mirrors. Members of
the audience stand behind and beside the cabinet all through
the performance. The assistant swings the mirrors against the
sides before be comes out the last time, and then members of
the audience are asked to examine the cabinet, when, of
course, they find nothing.
Illusion Show. Pharaoh's thumb. Make a table
out of cardboard (Fig. 95) and stand it on three legs, each of
which is exactly 5 1/4 inches from the other two, and place
your two mirrors between A and B and A
and C. Surround it by
screens on three sides, making the sides and
GILBERT LIGHT EXPERIMENTS 63
back exactly alike and exactly
the same distance from the table.
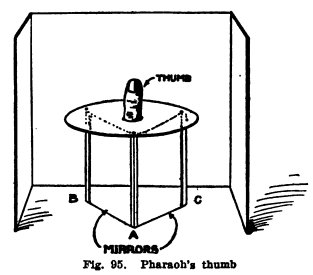
Now have an assistant put his
arm through a hole in the back curtain and put his blackened
thumb up through a hole in the table top, and you are ready to
begin the act.
Explain to the audience that you have succeeded in bringing to
life the thumb of an ancient pharaoh by your hypnotic power.
Explain that the thumb was lost in battle, fell on the sands
of the desert and dried but did not decompose. This pharaoh
was a great hypnotist, which makes it easier for you to bring
his thumb back to life. Explain also that the thumb will
answer any question about the future. If the thumb moves
forward it is, yes; if it doesn't move at all it is, no.
Now open the curtains, address the thumb, "O Thumb of an
ancient Pharaoh, awake! Awake! Awake!" (slowly and with
passes). The thumb does not move. You now ask, "O ancient and
sacred Thumb, will Charles get his wish?" (Thumb slowly nods,
yes.) "O ancient and sacred Thumb, will Henry get through his
examinations?" (Thumb does not move. No.) And so on.
Vaudeville Act. The
acrobat. You can put on a short but very funny act with a
mirror (Fig. 96) placed at an angle to the audience.
64 GILBERT BOY
ENGINEERING

FUN WITH THE CURVED
MIRROR
Experiment No. 54.
Converging sunlight.
Open the slit in your darkened
room to its full size and allow the sunlight to fall on the
concave (curved-in) side of your curved mirror. Make a dust.
Is the sunlight converged to a point and does it diverge
beyond this point (Fig, 97) ? This point is the focus of the
mirror.
Experiment No. 55.
Diverging sunlight.
Turn the convex (curved-out)
side of the mirror to the sunlight (Fig. 98). Is the sunlight
reflected and diverged or spread?
GILBERT LIGHT
EXPERIMENTS 65
Experiment No. 56.
Picture of the sun.
Remove the shutter, stand the
mirror on the table in the sunlight, and focus the sunlight on
a strip of paper 1/2 inch wide (Fig. 99). Is the picture of
the sun round and very bright?
Experiment No.57.
The focus is very hot.
Focus the sunlight on your
hand with the concave mirror (Fig. 100). Is it hot? It is,
because all the heat of the sunlight is concentrated at the
focus.
Experiment No. 58.
To light a match with sunlight.
Place a match in front of a
narrow strip of paper (Fig. 101) and focus the sunlight on the
head. Does the match light?
Experiment No. 59.
A magic cannon.
Stick a needle into the under
side of a cork and stick a match on the other end of the
needle (Fig. 108), with a small piece of paper at one side of
the head. Insert the stopper in an empty bottle, focus the
sunlight on the match head through the glass sides (Fig. 103).
Does the match light and are the cork, needle, and match
driven out with a satisfactory pop?
66 GILBERT BOY
ENGINEERING
The lighted match heats the
air and the expanding air drives out the cork.
Experiment No. 60.
Focal length of concave mirror.
Focus the sunlight on a narrow
piece of paper and measure the distance between the back
of the mirror and the paper. This is the focal length of the
mirror. Do you find it to be about two inches ?
Experiment No. 61.
Focal length of convex mirror.
Make two pencil dots just 3
inches apart on a piece of cardboard and between these punch
two holes just 1 inch apart. Hold the cardboard between the
convex mirror and the sun and move it until the light which
passes through the holes 1 inch apart is reflected to the dots
2 inches apart, and measure the distance from the back of the
mirror to the card. This is the focal
GILBERT LIGHT
EXPERIMENTS 67
length of the convex mirror.
Do you find it to be 2 inches?
There is no real focus for a
convex mirror because it spreads the light, but the
reflected rays appear to come from a point 2 inches
behind the mirror. An unreal focus of this kind is called
a virtual focus.
Experiment No. 62.
Pictures.
Go to the back of the room,
turn the concave mirror toward the window, and hold a piece of
paper three-quarters inch Wide near the focus (Fig. 104). Do
you find a small inverted picture in natural colors of the
window and of the things outside the window?
Have a friend move about near the window. Do you get his
picture?
68 GILBERT BOY
ENGINEERING

Experiment No.
63.
Your own image.
Look at yourself in the
concave mirror. Are you upside down and small? Bring your eye
closer to the mirror than the focus (3 inches) (Fig. 105). Is
your eye large and right side up? Look at yourself in the
convex side. Are you small and right side up in all cases?
THE "WHY" OF THE CURVED MIRRORS
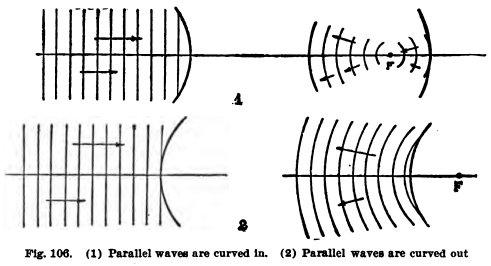
Waves. When parallel waves (1), Fig. 106,
strike the concave side of the mirror, they are reflected and
so curved in that they converge at the focus and then diverge.
When parallel waves strike the convex side (2), they are
reflected and so curved out that they diverge and never meet.
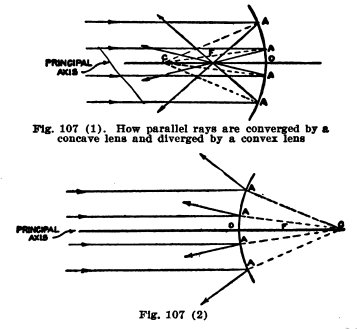
Rays. The curved mirror is part of a sphere
and the center of the sphere is at C, Fig. 107(1). The lines CA are radii of the sphere
and they are perpendicular to the mirror. When parallel rays
strike the concave mirror they make equal angles with these
perpendic-
GILBERT LIGHT
EXPERIMENTS 69
ular radii and cross at the
focus F. The line
through the center O
of the mirror and through the center C of the sphere is called
the principal axis of the mirror. You will notice that the
parallel
70
GILBERT BOY ENGINEERING
GILBERT LIGHT
EXPERIMENTS 71
rays which are above the
principal axis before they strike the concave mirror are below
it afterward and vice versa. This explains why the images you
see in the concave mirror are reversed.
When your eye is nearer than
the focus, it intercepts the rays before they can cross, and
your image appears to be behind the mirror, right side up and
large.
When parallel rays strike the convex side of the mirror.
Fig. 107 (2), they make equal angles with the radii (CA extended); they diverge
but appear to come from the focus F. This is the unreal or virtual focus.
The rays above the principal axis before reflection are above
it afterward, and, therefore, the images in the convex mirror
are right side up.
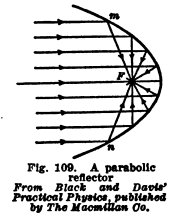
Searchlight Reflectors. The
reflectors
on battleship searchlights (Fig. 108) are made in the shape of
a parabola (Fig. 109). Parallel rays which strike parabolic
reflectors converge exactly at the focus, and conversely if a
light is placed exactly at the focus the reflected light
consists of parallel rays which go straight forward. The
reflectors on automobile and locomotive headlights are also
parabolic, and the lamp is placed at the focus.
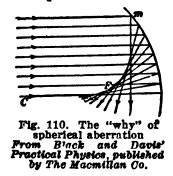
Spherical Aberration. Spherical mirrors do not
converge all parallel rays at the focus because those which
strike near the edge are reflected behind the focus (Fig.
110). This is called the spherical error or spherical
aberration of the mirror. Conversely if a light is placed at
its focus a spherical mirror does not reflect it in parallel
rays. This explains why it is not used as a first-class
reflector.
72 GILBERT BOY
ENGINEERING
REFRACTION OF LIGHT
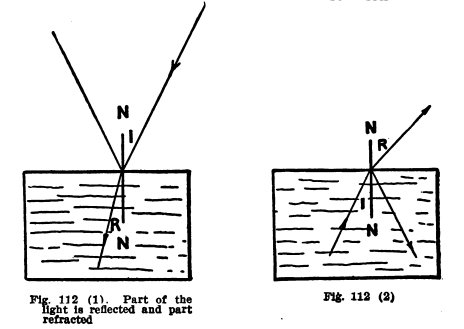
When light passes in a
slanting direction from one medium to another, - for example,
from air to water or the reverse, or from air to glass or the
reverse, - part of it is reflected at the surface between the
two media and part of it enters the second medium but is bent
out of its path, from ABC
to ABD, Fig. 111.
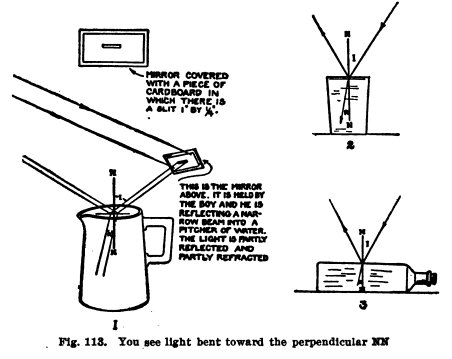
This bending is called refraction. When light passes from air
to any denser medium as water or glass, it is bent toward a
line NN drawn
perpendicularly through the surface at the point it enters.
See Fig. 112 (1). When light passes from water or glass to
air, it is bent away from the perpendicular NN. See Fig. 112 (2).
GILBERT LIGHT
EXPERIMENTS 73
FUN WITH SUNLIGHT
Experiment No. 64.
Air to water.
Allow a beam of sunlight to
pass through the slit in your darkened room. Cut a slit 1 inch
long and 1/4 inch wide in a piece of cardboard, put this over
your mirror, and reflect sunlight into a glass pitcher full of
water into which you have put 2 or 3 drops of milk (1), Fig.
113. Vary the slant of the beam of sunlight which strikes the
water and view the beam in the water through the sides of the
pitcher. Is some of the light reflected at the surface of the
water? Does some of it enter the water and is it bent or
refracted? Make the beam split on the side of the pitcher so
that half is inside and half outside. Is the beam in the water
bent toward an imaginary perpendicular at the point it enters?
Repeat this with a glass of milky water (2). Repeat with a
bottle of milky water (3). Use a bottle with flat sides.
74 GILBERT BOY
ENGINEERING
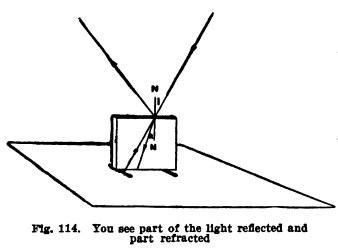
Experiment No. 65.
Air to glass.
Make the beam split on the
thick glass plate standing on its edge, on two matches, on
paper (Fig. 114). You cannot see the light in the glass but
you can see it on the paper below after it has passed through
the glass. Is the light which passes through the glass bent
toward an imaginary perpendicular NN drawn at the point it enters?
Let the sunlight enter through a slit 1 inch long and
1/4 inch wide. Split the beam of light on the edge of the
glass plate and hold a piece of paper behind the plate. Tilt
the plate to different angles. Is the light which passes
through the glass plate always bent toward the perpendicular NN?
Experiment No. 66.
A glass of
water.
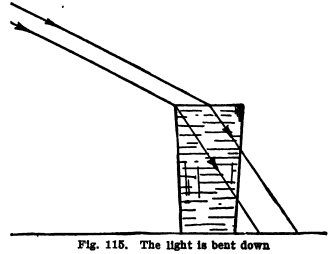
Remove your shutter and stand
a glass of water in sunlight near the window; fill the glass
to the top and put paper around the sides to keep out the
sunlight. Is the sunlight which strikes the water
GILBERT LIGHT
EXPERIMENTS 75
surface bent down, as shown in Fig. 116?
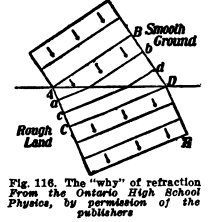
Explanation of Refraction. A beam of sunlight
is bent or refracted when it passes from air to water because
light travels more slowly in water than it does in
air. Its velocity in water is only three-fourths of its
velocity in air.
Now to see the connection between change in direction and
change in velocity, let us consider what would happen if
a regiment of soldiers marched in a slanting direction BD from
smooth ground to rough ground, as shown in Fig. 116. The men
would march less rapidly on the rough ground and the direction
of the marching lines would be changed. The line AB is still on smooth
ground and is straight. Part of the line ab is on rough ground and
this part is somewhat behind. The line cd has a larger part on
rough ground and this part is behind. The line CD is wholly on rough
ground and it is marching in a direction DE different from BD, and it would continue
in this new direction. This is exactly what happens to
parallel light waves. They are bent toward the perpendicular
when they pass at a slant from air to water or glass because
they travel more slowly in water or glass than they do in air.
They are bent away from the perpendicular when they pass at a
slant from water or glass to air because they travel faster in
air than they do in water or glass.
REFRACTION OF SPHERICAL WAVES
Experiment No. 67.
A coin under water.
Put a coin in a glass of water
and look down at it through the water (Fig. 117). Does it
appear to be nearer than it really is?
You see the coin because light passes from it to your eyes.
This light is in the form of spherical waves in the water, but
"The Science Notebook" Copyright 2008-2018 - Norman
Young
 The
Science Notebook
The
Science Notebook The
Science Notebook
The
Science Notebook